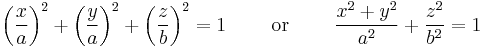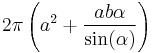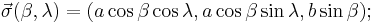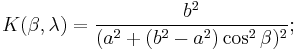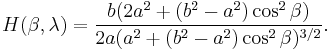Spheroid


oblate spheroid	prolate spheroid

A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters.

If the ellipse is rotated about its major axis, the result is a prolate (elongated) spheroid, like a rugby ball. If the ellipse is rotated about its minor axis, the result is an oblate (flattened) spheroid, like a lentil. If the generating ellipse is a circle, the result is a sphere.

Because of the combined effects of gravitation and rotation, the Earth's shape is roughly that of a sphere slightly flattened in the direction of its axis. For that reason, in cartography the Earth is often approximated by an oblate spheroid instead of a sphere. The current World Geodetic System model uses a spheroid whose radius is 6,378.137 km at the equator and 6,356.752 km at the poles.

1 Equation
2 Surface area
3 Volume
4 Curvature
5 See also
6 References
7 External links

Equation

A spheroid centered at the "y" origin and rotated about the z axis is defined by the implicit equation

$\left(\frac{x}{a}\right)^2%2B\left(\frac{y}{a}\right)^2%2B\left(\frac{z}{b}\right)^2 = 1\quad\quad\hbox{ or }\quad\quad\frac{x^2%2By^2}{a^2}%2B\frac{z^2}{b^2}=1$

where a is the horizontal, transverse radius at the equator, and b is the vertical, conjugate radius.^[1]

Surface area

A prolate spheroid has surface area

$2\pi\left(a^2%2B\frac{a b \alpha}{\sin(\alpha)}\right)$

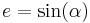where $\alpha=\arccos\left(\frac{a}{b}\right)$ is the angular eccentricity of the prolate spheroid, and $e=\sin(\alpha)$ is its (ordinary) eccentricity.

An oblate spheroid has surface area

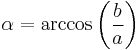$2\pi\left[a^2%2B\frac{b^2}{\sin(\alpha)} \ln\left(\frac{1%2B \sin(\alpha)}{\cos(\alpha)}\right)\right]$ where $\alpha=\arccos\left(\frac{b}{a}\right)$ is the angular eccentricity of the oblate spheroid.

Volume

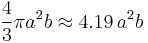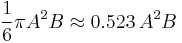The volume of a spheroid (of any kind) is $\frac{4}{3}\pi a^2b \approx 4.19\, a^2b$ . If A=2a is the equatorial diameter, and B=2b is the polar diameter, the volume is $\frac{1}{6}\pi A^2B \approx 0.523\, A^2B$ .

Curvature

If a spheroid is parameterized as

$\vec \sigma (\beta,\lambda) = (a \cos \beta \cos \lambda, a \cos \beta \sin \lambda, b \sin \beta);\,\!$

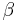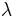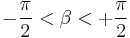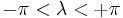where $\beta\,\!$ is the reduced or parametric latitude, $\lambda\,\!$ is the longitude, and $-\frac{\pi}{2}<\beta<%2B\frac{\pi}{2}\,\!$ and $-\pi<\lambda<%2B\pi\,\!$ , then its Gaussian curvature is